Gaussian Blur Evaluation
Approximate Gaussian Filter Evaluation
The Gaussian Blur filter algorithm is used in image processing to smooth over noisy images. They generally generate a new color value for each pixel by incorporating the color values of neighboring pixels, weighted depending on the distance between pixel and neighbor.
Precise implementations of the Gaussian blur algorithms calculate this by moving a sliding window over the image, adding up neighboring pixels (multiplied by weights).
We compare a precise implementation of the Gaussian blur algorithm with a 3x3 window (greyscale) to implementations using
- the Lookup Table
- the approximate ALU
Evaluation: Lookup Table
Implementation
The Gaussian LUT implementation passes over the image twice: once with a 3x1 window in the horizonal direction to generate an intermediate image, then with a 1x3 window in the vertical to generate the final pixel value. The lookup table is fed with the 3 most significant bits from each pixel value in the window.

Only the 3 most significant bits of each pixel in the window are fed into the lookup table to first look-up an intermediate result for the horizontal traveling window. Another lookup from the intermediate image returns the final value of each pixel.
Code for our Lookup Table implementation of the Gaussian filter algorithm
Approach
The application was run on a ml605 FPGA using the Makefile.
64x64, 128x128, 192x192 and 256x256 (below) images were processed with the LUT Gaussian application, each 20 times. The speedup was measured by cycle-counting in comparison to the precise Gaussian filter implementation. Standard deviation of the runtime was calculated.
The resulting approximate images were compared pixel by pixel to the output of the precise Gaussian filter implementation. Mean absolute and relative deviation were calculated from the differences and distributions of the absolute deviations were compiled for each image size.
Results
For a 256 by 256 pixel image, the original:

a precisely Gaussian-blurred version:

and an approximated Gaussian blur version, created with a Lookup Table with 9 inputs and 128 possible entries:

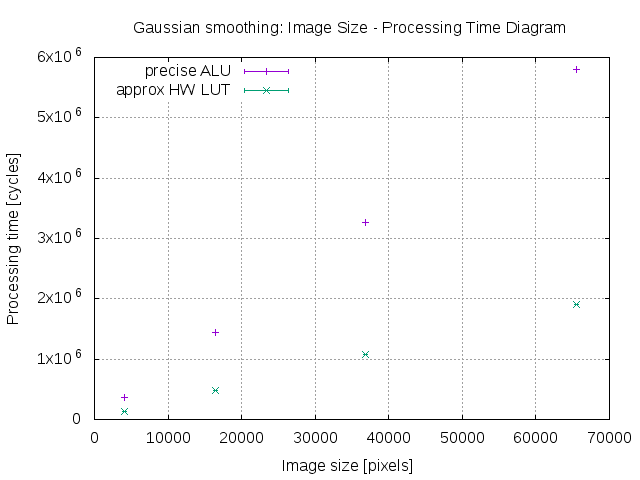
The Gaussian LUT speedup compared to the precise version was approximately 3, with slight improvements as image size rose. One standard deviation is marked in the graph but barely discernible.
| Image size | LUT Speedup |
|---|---|
| 64x64 | 2.934 |
| 128x128 | 3.003 |
| 192x192 | 3.032 |
| 256x256 | 3.044 |
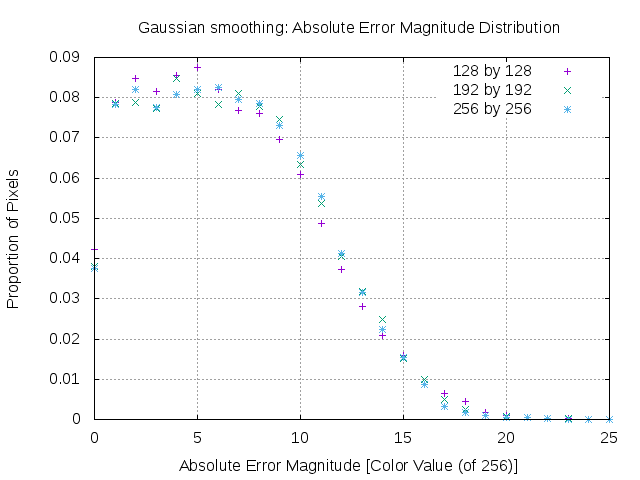
In comparison of the resulting images we found the following mean absolute and relative errors of grey values (0-255):
| Image size | Mean absolute error | Mean relative error |
|---|---|---|
| 64x64* | - | 0.04074 |
| 128x128 | 6.427 | 0.06617 |
| 192x192 | 6.587 | 0.06992 |
| 256x256 | 6.537 | 0.07129 |
* Star image, so not comparable with Lenna images.
We were suspicious of the rise in mean relative error with image size, so we decided to conclude with a histogram of error magnitudes:
Evaluation: Approximate ALU
Implementation
This implementation approximates the multiplication of one pixel with the filter kernel using mul.approx and the additions of the resulting values from each multiplication using add.approx. Other than that, it corresponds to the native implementation.
Linked: The complete code including a Makefile.
Approach
The application was run on a ml605 FPGA using the script run_eval.py. This script iterates over a Lenna image in three different sizes: 128x128, 192x192, and 256x256. For each iteration it applies the gaussian filter once using the native implementation and afterwards it applies the filter for each possible neglect amount combination the two instructions can have. An image is saved once for the native run and for each possible combination run using the following naming convention:
- Native -> native.png
- mul.approx with 2 bits neglected, add.approx not used -> MUL63.png
- add.approx with 4 bits neglected, mul.approx not used -> ADD62.png
- add.approx with 7 bits neglected, mul.approx with 4 bits neglected -> ADD60MUL62.png
Note: The values after MUL and ADD in the image name correspond to the decimal value of the binary neglect masks defined in the Design Document.
Results
The Table below shows the results for an image of the size 256x256 pixel. The first column of the table describes how many bits were neglected on a mul.approx instruction, the second column is likewise for add.approx instructions. A “ - “ means that a precise instruction was used. The third column is a calculation of the approximation error between the natively calculated image and the respective approximately computed image. The last column show the resulting image of the approximate calculation.
| MUL neclect amount | ADD neglect amount | Approximation error | Image |
|---|---|---|---|
| - | - | - |  |
| - | 2 | 0 |  |
| - | 4 | 0.0004360977 |  |
| - | 7 | 0.0025993256 |  |
| - | 10 | 0.0199205464 |  |
| - | 15 | 0.4975493702 |  |
| - | >15 | 1 |  |
| 2 | - | 0.0161600577 |  |
| 2 | 2 | 0.0161600577 |  |
| 2 | 4 | 0.0161600577 |  |
| 2 | 7 | 0.0185167734 |  |
| 2 | 10 | 0.0367156413 |  |
| 2 | 15 | 0.5161841232 |  |
| 2 | >15 | 1 |  |
| 4 | - | 0.1064377457 |  |
| 4 | 2 | 0.1064377457 |  |
| 4 | 4 | 0.1064377457 |  |
| 4 | 7 | 0.1064377457 |  |
| 4 | 10 | 0.1143191514 |  |
| 4 | 15 | 0.6022564094 |  |
| 4 | >15 | 1 |  |
| 7 | - | 0.7206358056 |  |
| 7 | 2 | 0.7206358056 |  |
| 7 | 4 | 0.7206358056 |  |
| 7 | 7 | 0.7206358056 |  |
| 7 | 10 | 0.7206358056 |  |
| 7 | 15 | 0.7403286548 |  |
| >7 | * | 1 |  |