Gamma Correction
Gamma correction is a pixel translation operation used in image processing. It takes each pixel of an image and exponentiates it with a constant - the Gamma, the result of which is multiplied with a normalization factor to yield the output pixel value.
Implementation
Gamma correction can be implemented in a number of ways. For demonstrating and
evaluating the PACO LUT core, three implementations were used in comparison.
Input images are expected to use 24 bits per color component, 72 bits per pixel
in total.
The implementation itself uses a gamma exponent of 1.99 and a normalization
factor of 1.
PACO LUT implementation
The PACO LUT implementation uses a lookup-table of 128 values and performs linear interpolation with an additional 12 bits of the input flowing into interpolation.
Software Lookup-table
To speed up gamma correction evaluation at the cost of memory usage, one can
take advantage of the limited bit width of image data.
In common image formats, each color component is represented with 8 bits of
data, thus such a lookup-table would require 256 entries, each 8 bit wide.
For high-quality images of 24 bits per color already require more than 48 MiB
of lookup-table data.
To serve as a viable comparison with the PACO LUT implementation, this approach
was implemented on the Rocket SoC as well.
Trivial implementation
The trivial method of converting pixel values to floating-points, applying the
aforementioned operation and re-encoding the result to the output format.
This approach is easy to implement but takes the most processor time for
computation.
Due to complications with the floating-point unit on the Rocket SoC, this
implementation was executed on the host machine and used for quality reference.
Comparison of results
Visual comparison
Below you can find a visual comparison of algorithm output for a test image with
a resolution of 512 by 512 pixels and 8 bits per color channel. The image shows
from left to right: Original image, output of the PACO LUT implementation,
output of the Software Lookup-table and the reference output done by the
trivial implementation.
 To the naked eye, the results of all three implementations are almost identical.
In fact, the bit values only differ in the least significant bits.
To the naked eye, the results of all three implementations are almost identical.
In fact, the bit values only differ in the least significant bits.
Numerical comparison
For a numerical comparison, the PACO LUT was evaluated for a uniform subset
of the entire input domain: Values 0, 16, 32, …, 224.
The return values are compared to exact results obtained through the trivial
algorithm. To ensure the precision of the reference value, computation was
performed using MPFR floating-point numbers with 1024 significant bits.
This experiment was conducted for different gamma values (0.05, 0.75, 1.25,
1.99). The results of the experiments can be found in the table and figure
below (percentages are relative 224):
| gamma | mean absolute deviation | maximum deviation |
|---|---|---|
| 0.05 | 0.03576% | 69.24086% |
| 0.75 | 0.02187% | 0.27297% |
| 1.25 | 0.02597% | 0.09758% |
| 1.99 | 0.02489% | 0.09829% |
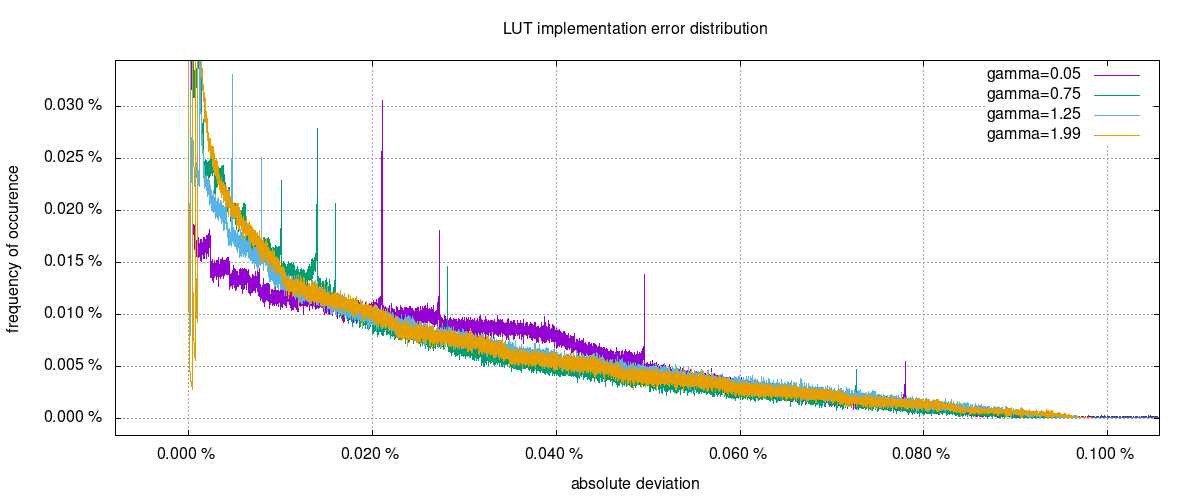 The error distribution was scaled to show the interesting subset. Outliers to
the right do not exceed 0.001%. The figure shows a significant dependency
between the gamma exponent and error distribution, however error magnitude
occurences converge to 0 at a magnitude of about 0.1%.
The error distribution was scaled to show the interesting subset. Outliers to
the right do not exceed 0.001%. The figure shows a significant dependency
between the gamma exponent and error distribution, however error magnitude
occurences converge to 0 at a magnitude of about 0.1%.
Timing comparison
In this comparison, clock cycles were counted in the computation of gamma
correction with different algorithms.
The table below shows the number of cycles elapsed during the computation of
various input pixels. For each input pixel the value is retrieved from memory
and then subjected to the gamma correction computation.
The first column shows cycles elapsed without any computation (just memory
retrieval), the second one shows time required by the software lookup-table,
followed by the PACO LUT implementation.
The final column shows the speedup in clock cycles and, in parentheses, the
speedup accounting for memory retrieval overhead.
| inputs | memory fetch only | software LUT | PACO LUT | speedup (computation only) |
|---|---|---|---|---|
| 8 | 620 | 843 | 780 | 1.0808 (1.3938) |
| 16 | 1127 | 1589 | 1463 | 1.0861 (1.3750) |
| 32 | 2183 | 3109 | 2855 | 1.0890 (1.3780) |
| 64 | 4295 | 6149 | 5639 | 1.0904 (1.3795) |
| 128 | 8519 | 12229 | 11207 | 1.0912 (1.3802) |
| 256 | 16967 | 24389 | 22343 | 1.0916 (1.3806) |
| 512 | 33863 | 48709 | 44615 | 1.0918 (1.3808) |
| 1024 | 67655 | 97349 | 89159 | 1.0919 (1.3809) |
| 2048 | 135239 | 194629 | 178247 | 1.0919 (1.3809) |
| 4096 | 270407 | 389189 | 356423 | 1.0919 (1.3809) |
| 8192 | 540743 | 778309 | 712775 | 1.0919 (1.3809) |
| 16384 | 1081415 | 1556549 | 1425479 | 1.0919 (1.3809) |
| 32768 | 2162759 | 3113029 | 2850887 | 1.0920 (1.3809) |
| 65536 | 4325447 | 6225989 | 5701703 | 1.0920 (1.3810) |
| 131072 | 8650823 | 12451909 | 11403335 | 1.0920 (1.3810) |
| 262144 | 17301575 | 24903749 | 22806599 | 1.0920 (1.3810) |
| 524288 | 34603079 | 49807429 | 45613127 | 1.0920 (1.3810) |
| 1048576 | 69206087 | 99614789 | 91226183 | 1.0920 (1.3810) |
| 2097152 | 138412103 | 199229509 | 182452295 | 1.0920 (1.3810) |
| 4194304 | 276824135 | 398458949 | 364904519 | 1.0920 (1.3810) |
This data shows a linear relationship between inputs and processing time for
all executions and a speedup of approximately 1.38 of the PACO LUT relative
to the fastest native implementation (software-based lookup-table).
It shows that through cache misses and subsequent memory lookup overhead, the
single-instruction PACO LUT execution outperforms the software solution in terms
of speed of execution.
Reconfiguration overhead
Both the software and PACO LUT implementations do not directly compare to the
trivial implementation as they involve ahead-of-time knowledge of the gamma
exponent and corresponding precomputation of data.
In the following we analyze the penalty of re-computing a lookup table for
8 bits of input data (256 value Lookup table).
The PACO LUT uses up to 19 bits of information to compute its output ( 7 bits
of segment addresses and 11 bits of interpolation ) thus the full 256 possible
inputs must be computed to adjust the LUT for a new gamma value.
In addition to this, the raw data points must be translated to base and
incline values for the PACO LUT.
To test the overhead of reconfiguration, a fixed-point implementation of the trivial algorithm was written to be run on the Rocket SoC. While this implementation is very slow, it gives a rough estimation of reconfiguration overhead. The table below shows reconfiguration time and speedup for reconfiguration with various gamma values:
| gamma | fixedpoint computation | software LUT | PACO LUT | speedup |
|---|---|---|---|---|
| 0.1875 | 4282067 | 4291503 | 4301724 | 1.00 |
| 0.3750 | 4621677 | 4646191 | 4654250 | 1.00 |
| 0.5625 | 4918827 | 4912637 | 4941795 | 1.01 |
| 0.7500 | 5118668 | 5137432 | 5128493 | 1.00 |
| 0.9375 | 5357255 | 5359153 | 5405529 | 1.01 |
| 1.1875 | 5739910 | 5738189 | 5774236 | 1.01 |
| 1.3750 | 5945458 | 5935402 | 5981904 | 1.01 |
| 1.5625 | 5902792 | 5901757 | 5932537 | 1.01 |
| 1.7500 | 5532115 | 5536970 | 5559159 | 1.00 |
| 1.9375 | 4815349 | 4820213 | 4842020 | 1.00 |
We see that the reconfiguration overhead for both LUT versions are roughly
equal and the majority of time is consumed during fixedpoint computation.
Due to a jitter in the computation it is not possible to state accurate
comparisons of configuration time without computation time.
Using data from the timing comparison we also see that during recomputation
using fixed-point values, about 49 to 69 thousand pixels could have been
processed with the PACO LUT (45 to 63 thousand using the software LUT).
This corresponds to a greyscale image of about 256 by 256 pixels.
Conclusion
We have seen that gamma correction can be approximated very efficiently using the PACO LUT implementation. Compared to software-based lookup-table implementation, which consists of only a single lookup, a speedup of 38% was achieved while keeping the approximation error below 0.1%.